План-конспект уроку у 11-А класі
Клименко Г.В.
Тема уроку: Степенева функція
Мета уроку: Систематизувати відомості про степеневу функцію, показник якої число:
ü натуральне;
ü ціле;
ü дробове.
Узагальнити властивості функції та формувати навички побудови графіка степеневої функції. Розвивати графічні навички, логічне мислення, увагу, пам’ять.
Формувати навички самостійної праці, вміння застосовувати набуті знання на практиці.
Обладнання: Комп’ютер, проектор.
“Деякі види трансцендентних функцій, які найбільш
часто зустрічаються, найперше степеневі та показникові, відкривають доступ до багатьох досліджень”
Л. Ейлер
План-конспект №2.docx (54962) Степенева функція, її властивості, графік. Побудова графіка степеневої функції різними способами.
План-конспект уроку алгебри
У 9-му класі СЗШ
вчителя математики
Швець Ірини
Тема. Степенева функція
Мета уроку. Познайомити учнів із степеневою функцією, її властивостями і графіками.
І. Перевірка домашнього завдання
1. Перевірити наявність виконаного домашнього завдання.
2. Розв'язування вправ.
а) Обчислити 
. Відповідь: 5.
б) Спростити вираз 
. Відповідь: ab.
в) Спростити вираз 
. Відповідь: 2a.
II. Сприймання і усвідомлення матеріалу про степеневу функцію
Степеневою функцією називається функція виду у = хp, де р — постійне дійсне число, а х (основа) — змінна. Згадаємо властивості степеневих функцій, їхні графіки. Результати наших досліджень будемо записувати в таблицю.
План-конспект №3.doc (230912) Дослідження похідної алгераїчних(трансцендентних) функцій.
Борздих Анна Романівна Студентка ВДПУ
Інституту математики, фізики і технологічної освіти
3-АМ групи
Тема уроку: Дослідження функції за допомогою похідної та побудова її графіка.
Мета уроку: Познайомити учнів із загальною схемою дослідження функцій.
Сформувати вміння та навички дослідження функцій за допомогою похідної та побудови їх графіків.
Розвивати алгоритмічне й логічне мислення, самостійно приймати рішення.
Виховувати пізнавальний інтерес до предмета комп’ютерної техніки, позитивну мотивацію до навчання.
Тип уроку: урок засвоєння нових знань.
Місце проведення: комп’ютерний клас.
Методичне забезпечення: правила поведінки і ТБ у кабінеті, програма
дослідження функції, тести для перевірки, комп’ютерна презентація уроку, музей картин «Прекрасних ліній».
Епіграф: Скажи мені - і я забуду,
Покажи мені – і я запам’ятаю,
Дай мені діяти самому – і я навчуся…
Китайська народна мудрість
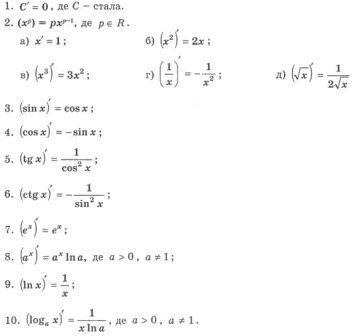
План-конспект №4.docx (60303) Логарифмічна функція, її властивості та графік.
План-конспект уроку алгебри
У 9-му класі СЗШ
вчителя математики
Швець Ірини
Тема. Логарифмічна функція, її графік і властивості
Способи побудови графіка логарифмічної функції
Мета уроку. Ознайомити учнів з логарифмічною функцією, її властивостями і графіком.
І. Перевірка домашнього завдання
1. Три учні відтворюють розв'язування вправ № 13, 15, 20.
2. Розв'язування вправ, аналогічних домашнім.
II. Аналіз самостійної роботи, проведеної на попередньому уроці
III. Засвоєння властивостей логарифмічної функції та її графіка
Функція виду у = loga x, де а — задане число, а > 0, а ≠ 1 називається логарифмічною функцією.
Логарифмічна функція має такі властивості:
1) Область визначення функції — множина всіх додатних чисел. Ця властивість випливає із означення логарифма, оскільки вираз loga х має смисл тільки при х > 0.
2) Область значень логарифмічної функції — множина R усіх дійсних чисел. Ця властивість випливає з того, що для будь-якого дійсного числа b є таке додатне число х, що logax = b, тобто рівняння loga x = b має єдиний корінь. Такий корінь існує і дорівнює х = аb, оскільки loga аb = b.
3) Логарифмічна функція на всій області визначення зростає (при а > 1) або спадає (при 0 < а < 1). Нехай а > 1. Доведемо, що якщо x2 > х1 > 0, то
loga х2 > loga x1. Користуючись основною логарифмічною тотожністю, умовою x2 > х1, можна записати . З останньої нерівності за властивістю степеня з основою а > 1 маємо, що loga х2 > loga x1.
Нехай 0 < а < 1. Доведемо, що якщо x2 > х1 > 0, то logaх2 < loga x1. Записавши умову x2 > х1 у вигляді одержуємо loga х2 < loga x1, оскільки 0 < а < 1.
4) Якщо а > 1, то функція у = loga x приймає додатні значення при х > 1, від'ємні — при 0 < х < 1. Якщо 0 < а < 1, то функція у = loga x приймає додатні значення при 0 < х < 1, від'ємні — при х > 1.
План-конспект №5.docx (73929) Показникова функція, її властивості та графік. Основні способи побудови показникової функції
План-конспект уроку алгебри
У 9-му класі СЗШ
вчителя математики
Швець Ірини
Тема. Показникова функція, її графік і властивості
Мета уроку. Засвоєння учнями поняття показникової функції, її властивостей і графіка.
Обладнання. Таблиця «Показникова функція».
І. Аналіз контрольної роботи
II. Повідомлення теми уроку
III. Сприймання і усвідомлення нового матеріалу
Функція виду у = ах, де а > 0, а ≠ 1, називається показниковою (з основою а).
Усне виконання вправ
1. Які із поданих функцій є показниковими:
а) у = 2х; б) у = х3; в) у = (-5)х; г) у = ()х; д) у = (0,3)х; е) у = nх?
Відповідь: а); г); д); е).
2. Наведіть приклади показникових функцій.
План-конспект №6.docx (141916) Тригонометричні функції числового аргументу
План-конспект уроку алгебри
У 9-му класі СЗШ
вчителя математики
Швець Ірини
Тема. Тригонометричні функції числового аргументу
Мета уроку: Формування поняття тригонометричних функцій числового аргументу; вивчення значень тригонометричних функцій деяких чисел (кутів), зміни знаків тригонометричних функцій у координатних чвертях.
Література:
1. Навчальний посібник "Математика у старшій школі"/К. Карпік.-2012.-січень
2. Бондар Г. М. Методи і способи розв*язування трансцендентних рівнянь з параметрами: Урок0-проект 11 клас/Г.М Бондар// Математика в школах України.-2007.травень(№13-14)
-ст. 57-62
3. Журнал "Математика в школах України"
Плани розроблялися на основі шкільних підручників:
1. Підручник Алгебра-9 Істер
2. Підручник Алгебра-11 Мерзляк, Полонський і Якір